
Jeder Artikel auf dieser Seite wurde von einem Herausgeber von House Beautiful von Hand ausgewählt. Wir können Provisionen für einige der Artikel verdienen, die Sie kaufen möchten.
Es gibt nichts Vergleichbares zu einem verrücktes mathematisches Problem, umwerfende optische Täuschung, oder Twisty Logic Puzzle alle Produktivität in der stoppen Beliebte Mechanik Büro. Wir sind von Natur aus neugierige Menschen, aber wir teilen auch gemeinsam ein hartnäckiges Bestehen, das wir sind richtig, verdammtund so neigen wir dazu, die Arbeit auf der Strecke zu lassen, wenn wir auf ein Problem mit mehreren scheinbar möglichen Lösungen stoßen.
Dieser dreieckige Rätsel ist nicht neu Popsugar zum es ausgraben Vor ein paar Jahren - aber basierend auf etwas zwielichtiger Internet-Magie - tauchte der unten stehende Tweet heute in meinem Feed wieder auf und löste eine neue Debatte über unser gesamtes Personal aus Slack Channel, ein Ort, der traditionell für Workshopping-Ideen reserviert ist, aber hauptsächlich dazu dient, über andere Dinge zu schreien, in die wir uns gelegentlich verwandeln Inhalt.
Sagen? pic.twitter.com/lrhXrWw5EP
- J (@jiteshpillaai) 9. April 2018
Da ich ein Masochist bin, habe ich das Dreieck noch einmal gezeichnet und alle Mitarbeiter gebeten, das, was sie taten, umgehend fallen zu lassen und zu versuchen, die einfache Frage zu lösen: Wie viele Dreiecke kannst du finden?
Ich werde Ihnen das gesamte Gespräch ersparen - vertrauen Sie mir, niemand möchte das sehen -, aber die Antworten des Teams waren weit verbreitet. Einige Redakteure sahen vier Dreiecke. Andere sahen 12. Einige sahen 6, 16, 22. Noch mehr sahen 18. Ein wiseguy zählte die Dreiecke in den A’s in der Frage selbst, während ein anderer existenziell zu sein schien Krise: "Keine dieser Linien ist wirklich gerade, nur Kurven - daher kann man keine von ihnen als Dreieck definieren", sagte er sagte. „Auf diesem Foto sind keine Dreiecke zu sehen. Das Leben hat keinen Sinn. “
Wir stellten das Problem dann unseren Instagram-Followern, deren Antworten ebenfalls den Ton angaben, von 5 auf 14 auf 37. Obwohl wir die hohe Wahrscheinlichkeit eines Trolling hier anerkennen, ist es klar, dass die Menschen auf viele verschiedene Arten auf das Problem reagieren.
Diesen Beitrag auf Instagram anzeigen
Bitte hören Sie auf, was Sie tun, und helfen Sie uns, eine Debatte zu lösen, die wir im Büro führen. Wie viele Dreiecke sehen Sie hier?
Ein Beitrag geteilt von Popular Mechanics Magazine (@popularmechanics) auf
Ich hätte meinen Kollegen den ganzen Tag zuhören können, wie sie ihre fragwürdigen Prozesse erläuterten. Stattdessen habe ich mich an mehrere Geometrieexperten gewandt, um zu einer Konsensantwort zu gelangen. Es stellte sich heraus, dass praktisch alle Mathematiker, mit denen ich Kontakt aufnahm, die gleiche Lösung fanden - aber nicht alle haben es auf die gleiche Weise herausgefunden.
Wenn Sie die Antwort noch nicht wissen möchten, hören Sie auf zu lesen und versuchen Sie zuerst, das Problem zu lösen. Ich treffe Sie hier wieder, wenn Sie fertig sind.
Hey, das ging schnell. Bereit für die Antwort? Im Gegensatz zu einigen virale mathematische Probleme Diese sind absichtlich vage und offen für Interpretationen. Tatsächlich hat sie eine Slam-Dunk-Lösung, bei der es keinen Zweifel gibt, und das ist es auch 18. Lassen Sie uns von einigen Geometrieexperten erfahren, warum.
„Ich würde das so angehen, wie man sich einem mathematischen Problem nähert: Reduzieren und Struktur finden“, sagt er Sylvester Eriksson-Bique, Ph. D., Postdoc an der University of California in Los Angeles Abteilung.
Die einzige Möglichkeit, in der von mir gezeichneten Figur Dreiecke zu formen, besteht laut Erikkson-Bisque darin, dass der obere Scheitelpunkt (Ecke) Teil des Dreiecks ist. Die Basis des Dreiecks muss dann eine der drei Ebenen darunter sein. „Es gibt drei Ebenen und auf jeder kann man eine Basis aus sechs verschiedenen Möglichkeiten auswählen. Das ergibt 18 oder 3 mal 6 Dreiecke. “
Schauen wir uns noch einmal das Master-Dreieck an.
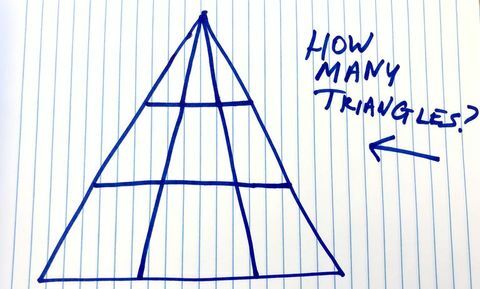
Andrew Daniels
"Es ist bequem, auf den Fall zu verallgemeinern, wo es gibt n Linien, die durch den oberen Scheitelpunkt verlaufen, und p horizontale Linien “, sagt Francis Bonahon, Ph. D., Professor für Mathematik an der University of Southern California.
In unserem Fall, n = 4 und p = 3. Jedes Dreieck, das wir in der Zeichnung finden, sollte einen oberen Eckpunkt und zwei andere auf derselben horizontalen Linie haben, also für jede horizontale Linie die Anzahl der Dreiecke mit Laut Bonahon entsprechen zwei Scheitelpunkte auf dieser Linie der Anzahl der Möglichkeiten, wie wir diese Scheitelpunkte auswählen können - nämlich der Anzahl der Möglichkeiten, aus denen wir zwei verschiedene Punkte auswählen können n, oder "n wähle 2. “
Erinnerst du dich an die High School Mathe? Das ist n(n-1)/2. Und da gibt es p horizontale Linien, sagt Bonahan, das gibt p n(n-1) / 2 mögliche Dreiecke. In unserem Fall ist das 3x4 (4-1) / 2 = 18.
Im Folgenden finden Sie eine praktische Aufschlüsselung, wie Sie jedes mögliche Dreieck finden:
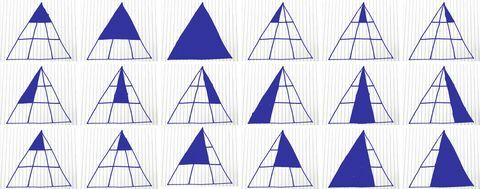
Kory Kennedy
Johanna Mangahas, Ph. D., eine stellvertretende Mathematikprofessorin an der Universität in Buffalo, wurde ebenfalls 18 - zuerst durch einfaches Brute-Force-Zählen, dann durch dasselbe Geschick Kombinatorik wie oben - aber wir geben zu, dass unser Dreieck-Rätsel nicht ganz so cool ist wie dieser von Po-Shen Loh, Ph. D., einem Mathematikprofessor an der Carnegie Mellon University in Los Angeles Pittsburgh, as in der vorgestellten New York Timesvergangenes Jahr:
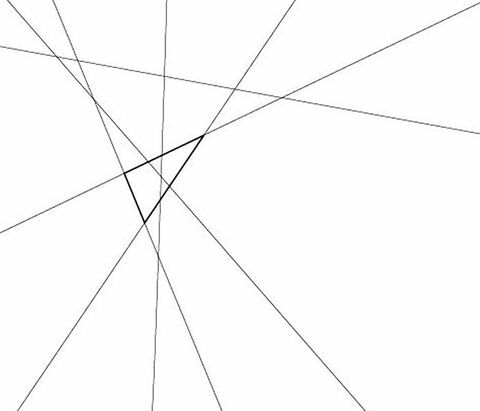
Po-Shen Loh
Die mathematische Antwort ist klüger, sagt sie, denn hier ist das Zählen von Dreiecken dasselbe wie das Zählen von Kombinationen von drei aus sechs ausgewählten Linien. [6-choose-3 = (6 * 5 * 4) / (3 * 2 * 1)].
„In diesem Fall schneidet sich jedes Linienpaar und es gibt keine Dreifach- oder Mehrfachkreuzungen. Daher ergibt jede Auswahl von drei immer ein Dreieck“, sagt Mangahas. Auf dem Bild, das ich ihr gesendet habe, sind einige Linien parallel, sodass sie nicht Teil desselben Dreiecks sein können. "Wenn Sie die gleichen sieben Zeilen genommen und sie ein wenig durcheinander gebracht hätten, wären sie wahrscheinlich am wahrscheinlichsten Land wie [Lohs] Problem und du hättest mehr Dreiecke und eine ähnliche süße Antwort. "(Für das Protokoll: 35.)
Wütend. Ich habe dieses neue Dreiecksproblem noch nicht mit meinen Kollegen geteilt. Aber es ist nur eine Frage der Zeit, bis sie es entdecken - und darüber streiten.
🚨WICHTIGES UPDATE 30.01.20🚨: Seit der Veröffentlichung dieser Geschichte haben viele, viele Die Leser haben sich bemüht, mir mitzuteilen, dass 18 in der Tat eine akzeptable Antwort auf dieses Problem ist, aber nicht die nur Zum einen, weil ich versehentlich etwas übersehen habe. Ich hätte es den Lesern viel leichter machen können - und vor allem meinem Posteingang -, hätte ich das Dreieck einfach auf weißem Computerpapier skizziert. Aber nein.
Ich habe dieses Dreieck leider auf liniertes Papier gezeichnet, und viele kluge Leute haben richtig darauf hingewiesen, dass tatsächlichZählt man die hellblauen parallelen Linien im Bild zusätzlich zu den dunkelblauen Linien in der Markierung, gibt es hier tatsächlich mehr als 18 Dreiecke insgesamt - erheblich mehr. Ich habe nie angegeben, nur diese dunkelblauen Linien zu verwenden, und daher irre ich mich. Du hast recht.
Ein Leser, Ralph Linsangan, hat mich vollständig in Besitz genommen, indem er dieses Bild gesendet hat, in dem er jedes zusätzliche Dreieck markiert, das unter der Technik gefunden wurde, und 17 zusätzliche Dreiecke für insgesamt 35 markiert. Erblicken:
Diese Art von Engagement ist nur einer von vielen Gründen, die ich liebe Beliebte Mechanik Leser. Wir können nichts an euch vorbei bringen. Bis zum nächsten Teaser!
🚨NOCH EIN ANDERES TRIANGLE UPDATE 31.01.20🚨: Seit dem letzten Update habe ich von Even gehört Mehr von dir, tadeln Sie mich - und Ihre Mitleser - weiterhin, weil Sie keine zusätzlichen möglichen Dreiecke in Betracht gezogen haben. Lassen Sie uns von Leser Derek Schneider hören, der eine weitere Grafik eingesandt hat, die vorschlägt, dass es 45 Dreiecke gibt.
Wenn wir jedoch die ursprünglichen Regeln befolgen, zähle ich und zusätzlich 9, die eindeutig sind (in grün) und eine, die es könnte Seien Sie offen für Interpretationen, je nachdem, wie Sie den oberen Scheitelpunkt (in Lila) visuell platzieren. Ich würde persönlich zählen es.

Derek Schneider
Leser Poingly schrieb in der Zwischenzeit, dass wir einen "gravierenden Fehler" beim Zählen der Dreiecke gemacht haben:
Nehmen Sie die untere rechte Ecke, sie zeigt zum Beispiel einen Pfeil für ein Dreieck. Es ist jedoch denkbar, dass diese hellblauen Linien allein in dieser einen Ecke bis zu DREI Dreiecke bilden:

Poingly
Während einige von diesen etwas umstritten sein KÖNNTEN (dh, wo GENAU die hellblauen Linien die dunklen schneiden und tun) sie bilden technisch gesehen ein Dreieck oder ein Viereck), ich habe SIEBEN ZUSÄTZLICHE Dreiecke gezählt, die in diesem gemacht werden können Weg. Dies erhöht die Gesamtzahl der Dreiecke auf 42.
Die schlechte Nachricht ist, dass wir einige Dreiecke verpasst haben. Die gute Nachricht ist, dass dies bestätigt, dass das Leben eindeutig einen Sinn hat, wie die genaue Zahl belegt: 42.
Hervorragender PunktPoingly. Leser James Goodrich ging noch einen Schritt weiter und schlug vor, dass wir uns überlegen sollten, was ein Dreieck sein könnte:
Nun, laut Ihrem Leser, der 17 zusätzliche Dreiecke hervorhob (unter Verwendung des "Andrew hat es nicht getan") angeben, welche Linien die 3 Kanten eines Dreiecks umfassen können ("Klausel), konnte nicht eindeutig eine ganze Menge finden Mehr. Nehmen Sie zum Beispiel das Mini-Dreieck unten links im Nachtrag "Wichtiges Update" vom 30. Januar 2020. Würden nicht die Bereiche des Minidreiecks und der angrenzende Bereich der Raute zusammen ein weiteres Dreieck ergeben?
Eine weitere Überlegung: Dreiecke haben 3 Winkel (wer hätte das gedacht?); Ich würde jedoch postulieren, dass die Beschreibung eines Dreiecks mit diesen Winkeln verschiedene Dreiecke erzeugen würde. Bei einem Dreieck T mit den Eckpunkten A, B und C könnte t-one tatsächlich durch ABC beschrieben werden, wobei B der zentrale Winkel ist. Ich schlage vor, dass t-two, das von BAC beschrieben wird, anders ist. Ähnliches gilt für BCA.
Wenn wir dann in einem bestimmten Fall rechtwinklige Dreiecke nehmen, können wir Sinus-, Cosinus- und Tangensfunktionen (SOH, CAH, TOA) ableiten. Wenn wir dies auf das Dreieck anwenden (und die Winkelanforderung lockern würden, könnte dies bedeuten, dass sich BAC von CAB unterscheidet. Natürlich werden Ausnahmen für isoskolische und gleichseitige Dreiecke gemacht (letztere hätten nur 3 verschiedene Dreiecksdefinitionen).
Ich habe nicht genau darüber nachgedacht, wie ich jeden Vorschlag quantifizieren soll (und die Anwendung des letzteren nach dem ersteren würde die Anzahl erhöhen) Ich habe also keine einfache Nummer für Sie, die Sie in einem aktualisierten wichtigen Update verwenden können (wenn Sie meine Ideen für sinnvoll befunden haben) aktualisieren).
Ich habe es getan, James. Und ich werde warten. Widerwillig entschloss ich mich, ein letztes Mal herauszufinden, wie viele zusätzliche Dreiecke unsere neuen chaotischen Regeln enthalten könnten, und kam auf 43 für insgesamt 61:
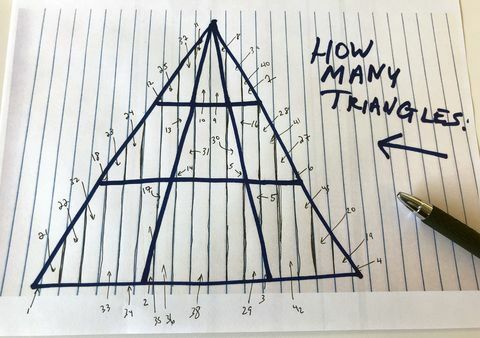
Andrew Daniels
Ich bin mir jedoch ziemlich sicher, dass jemand, der dies liest, mir sehr schnell sagen wird, dass ich mich erneut geirrt habe, und einen Beweis liefern wird von noch mehr versteckten Dreiecken, die mich auf dem langen und kurvenreichen Weg zu einem weiteren Kaninchenbau schickten Wahnsinn. (Randnotiz: Ich habe meine Frau seit drei Tagen nicht gesehen. Bitte sag ihr, dass ich sie liebe.) Ich stelle also eine letzte Herausforderung: Wenn Sie im Originalbild die bestmöglichen Dreiecke finden, zeigen Sie mir Ihre Arbeit und beweisen Sie dies definitiv Ihre Vormachtstellung, ich werde diese Geschichte ein letztes Mal aktualisieren und Sie zum König oder zur Königin des Dreiecks krönen für immer. Godspeed.

SpeedRipper Rubik's Cube
$12.45
Der Zauberwürfel macht die Menschen seit 40 Jahren wahnsinnig. Versuchen Sie es selbst herauszufinden, oder lernen, wie man es löst mit mathematik.

Kanoodle 3-D Puzzle-Spiel
$8.79
Mit nur 12 Teilen und insgesamt 200 Herausforderungen wird Kanoodle sowohl Kinder als auch Erwachsene mit 2-D- und 3-D-Puzzles überraschen.

Sagrada Brettspiel
$29.98
In einem der besten Rätsel Brettspiele des Jahres, Sie und bis zu drei andere Spieler versuchen, die Buntglasfenster der Sagrada Familia herzustellen.

Dimension 3-D Puzzle-Spiel
$40.97
Dieses rasante 3-D-Puzzlespiel kombiniert schnelles Denken, Logik und Glück, um die Kugeln zu stapeln und die meisten Punkte zu sammeln.
Von:Beliebte Mechanik


